Introduction
It is virtually impossible to produce high quality lentigrams without a deep knowledge of the lenticular medium. Unlike standard photography where the selection of the printing support commonly happens at the end of the process, in Lentigraphy it comes first. It is important to acknowledge the properties of a lenticular sheet at the start of the process to produce prints with intended depth, angle of view and clarity. Taking a series of pictures of an object and printing them onto a lenticular medium, ignoring its technical properties, will likely result in a print with shallow depth, lack of sharpness, banding, deformation and other undesired artifacts.
As shown in figure 1↑ a lenticular sheet is an array of plano-convex lenses which are commercially available in different sizes and formats.
The easy way to think of a lenticular sheet is like a projector composed by many small lenses. If a lenticular sheet is placed over a white back-lit display, each one of its plano‑convex lenses behaves exactly as a small projector, projecting anything printed on the back of the lens in the direction of the viewer. Any color dot printed on the flat side of a plano‑convex lens is magnified and projected in one specific direction like shown in figure 2↓.
Most of the properties of a plano-convex lens can be derived using standard Geometrical Optics where light is modeled with rays and their interaction with the lens surface fully described by the Law of Reflection and Snell’s Law of Refraction.
In a plano‑convex lens there is a special ray passing through the center of curvature of the lens and exiting undeflected and perpendicular to the curved surface: this is called the principal ray. A lenticular lens is built to project any small dot printed on the flat side of the lens as best as possible along the direction of the principal ray. For this reason a principal ray is a very good approximation to describe the lenticular sheet optic.
If we add more lenses adjacent to the original one these project the same pixel in different directions, far from the main direction the lens has been constructed for. These additional rays are artifacts produced by the lenticular medium and are responsible for the flipping (when the image repeat itself) observed when the viewer is outside the expected angle of view. These additional images, usually out of focus, cannot be removed.
If we now take a lenticular sheet, print behind it a repeating pattern of colors and draw all principal rays generated by every single color drop and passing through the center of curvature of each lens, we obtain something like shown in figure 4↓. The two different sets of rays are just two of the many different ways an image can be printed on a lenticular sheet but the second set gives some advantages which are shortly described here and in more detail later.
One reason the second set is to be preferred over the first one is because it allows a wider printing area behind each lens, this means that more lines can be printed behind each lens increasing the Lenticular Depth-of-Field, especially in big format prints. Another and more practical reason is that the second set of rays can be captured with a shorter rail or with a smaller camera array and last, but not less important, it guarantees a wider angle of view.
A lenticular manufacturer commonly describes a lenticular sheet with two quantities: the mechanical pitch
measured in LPI (Lenses Per Inch) and the angle of view
(see figure 5↓). These quantities are given as a general indication because they depend on the printing device and they often change slightly from stock to stock. For this reason they have to be checked against the target printing device with methods that will be described.
The angle of view
is a construction property of the lenticular sheet.
Light field
In this section I will introduce an important concept, the light field, that will be useful to understand how camera devices and lenticular media relate to each other in the realization of a 3D lentigram.
A physical object is visible either because it reflects back the environment light or because it is itself a light source. Part of the light hitting the object bounces off the surface and part penetrates its surface and is scattered around following laws dictated by the physical properties of the object. In first approximation, where incoherent light is used and where all objects in the scene are bigger than the wavelength of light, Geometrical Optics can be applied and all incident and reflected light can be modeled with rays of light as shown in figure 6↓.
A ray of light is essentially half of a line proceeding from an initial point, its source, and carrying with it information like intensity and color. With this idea in mind a light source can be modeled as a generator of rays. The simplest light source, a point light, can be modeled as a point in space which generates rays with the same intensity and color uniformly in all directions. Another source of light could be a surface with each of its points behaving like a set of point lights as displayed in figure 7↓.
When these rays hit a physical object, they interact with it and each point of the object itself becomes a source of rays. There are different and complex physical laws and principles to describe the interaction of a ray of light with an object but for the moment we are only interested in the basic principle that every single point on the surface of a physical object, or inside it, is a source of rays projected in different directions.
Within the boundaries of the Geometrical Optics approximation and in the context of 3D Lentigraphy we can define a light field as the set of all rays generated by every point of a physical object.
Based on this definition a photographic camera can be interpreted as a device that can capture a portion of the light field generated by a real object and a lenticular medium as a device that can generate a light field similar to the one produced by a real object.
It should be clear now that the aim of 3D Lentigraphy is to take pictures of an object from different angles to capture an approximation of its light field and to print these pictures onto a lenticular medium to generate a light field as close as possible to the original one. Figure 8↓ shows an array of 5 cameras used to capture a subset of the light field produced by a subject. A detail shows three points A, B and C, taken as an example, from which rays are partially captured by the cameras. It is clearly impossible to capture the whole light field because this would require an infinite number of cameras. For this reason interpolation methods are commonly used to build an approximation of the original light field from a limited amount of pictures.
Once the light field has been captured and reconstructed through interpolation, this basically means that a video has been created from the few pictures that have been taken, it is then transfered onto a lenticular sheet with a technique called interlacing. The interlacing algorithm, knowing all the optical parameters of a lenticular sheet and the position of all cameras, transfers all pictures on the lenticular sheet to match the generated light field with the original one produced by the real object (see figure 9↓). A viewer watching the lenticular print created in this way will observe a virtual 3D object that closely resembles the real one.
Optical pitch
A lenticular sheet is an array of plano-convex lenses, and each lens usually has a spherical profile with a center of curvature placed a distance
from the flat side of the lens. The optical pitch
is the distance between two adjacent centers of curvature projected onto the back plane of the sheet from the point of view of an observer placed at a distance
from the sheet. Figure 10↓ shows the projection of the centers of curvature of an array with few lenses. Because this is a central projection, the distance between consecutive projections is constant.
If
is the mechanical pitch, the size of a plano-convex lens and also the distance between two consecutive centers of curvature, it is clear that
It is also clear that
depends on the viewing distance
, the bigger the distance the smaller the optical pitch as shown in figure 11↑. When
is very large the optical pitch becomes equal to the mechanical pitch
The optical pitch depends only on the distance
, this means that if the viewer maintains a constant distance from the sheet and moves parallel to the sheet, the optical pitch doesn’t change as shown in figure 12↓
Effective angle of view
The angle of view
of a lenticular sheet is defined as the angle formed by two consecutive centers of curvature and the middle point measured on the back of the sheet. The angle of view is shown in figure 12↑ and is given by the formula
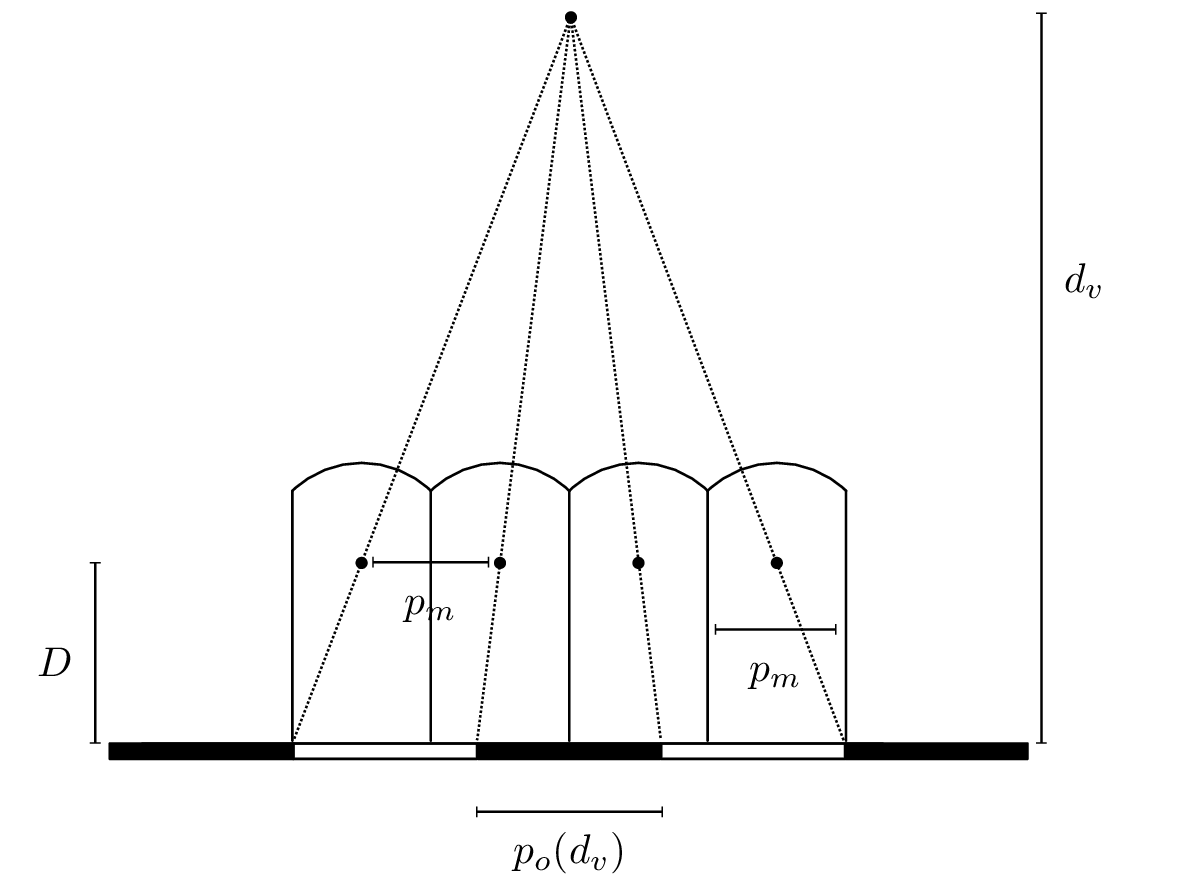
For a chosen distance
and a corresponding optical pitch
, if we print a pattern of colored dots on the back of the sheet at intervals of size
, this pattern will be visible by a viewer placed at the same distance
within the angle of view
before repeating itself again outside the angle as shown in figure 13↓.
If the pattern of dots represents a 3D picture, the viewer placed at the distance
will be able to observe the picture within the angle
and will notice a flip (the image repeating itself) just outside this angle. In figure 14↓ it is possible to see the different areas observed by a viewer at different observation points
,
,
,
,
and
all placed at the same distance
from the back of the lens.
The angle of view
is considered by many to be the effective angle of view experienced by a viewer: this is approximately true but there is a catch.
If we call
the effective observation angle, the angle over which a viewer can observe the 3D image before a flipping occurs, and
is the print viewing distance, planned at the time the image was interlaced and printed, we can prove the following
This means that the effective observation angle is equal to the angle of view only at a distance equal to the planned viewing distance. In figure 15↓ we show the angle of view
which is a construction property of the lens.
After choosing a distance
and the corresponding optical pitch
, a color pattern of size
is printed behind each lens. At distance
the effective angle of view
matches the angle of view
. Once the user comes closer with
, or moves back with
, we can see that the pattern repeats itself at an angle that is smaller than the angle of view
. The moment a flip occurs is highlighted with a red circle in both cases. At close distance the reduced visibility is apparent, at far distance it is mostly irrelevant.
Stereo base
Taking a 3D picture means taking a series of pictures of the same subject from different adjacent angles and printing the resulting sequence, in a special way, on a lenticular sheet. There are many ways to do it depending of the subject and the intended result.
- One common way is to use a fixed camera and to take pictures of a rotating subject.
- A second common way is to use a single camera mounted on a slider and to take pictures while the camera is sliding. Most of the time the camera is also pointing at the subject while sliding and a mechanical or electronic system is required to synchronize camera position and rotation.
- A third common way is to use an array of cameras and to take pictures of the same subject from different angle simultaneously.
No method is better than the other, the choice depending really on the situation, but all these methods require to calculate the positions/angles of the cameras at the extremes of the sequence. In the case of a rotating subject the problem is to find the initial and final angles of rotation. In the case of a camera array the problem is to find the position of the most extreme cameras. In the case of a sliding camera the problem is to find the initial and final positions of the camera on the slider.
In 3D lentigraphy the bounds are determined by the lenticular medium that the photographer plans to use. Each lens of a lenticular sheet projects every point that is printed on its back side into different directions based on some optical properties. For this reason it is required to take pictures from all possible viewing directions that each lens can project into.
To maximize the effective angle of view experienced by the viewer we’ve already shown that, behind the lenticular sheet, we need to print patterns of size
which depends on the planned viewing distance
.
We make for the moment the very important simplification that the photographer takes all pictures at a target distance
equal to the expected viewing distance
.
We call
the stereo base, the distance between the most extreme cameras in the case of an array of cameras or the total sliding distance of a single camera in the case of a slider. We call
the target or shooting distance, the distance between the camera and the subject or, to be more clear, the distance between the camera and what is assumed to be the stereoscopic window of the picture. The viewing angle of the lens is indicated with
.
As shown in figure 16↑, to cover all possible viewing directions for each single lens of the chosen lenticular sheet, the pictures has to be taken along the distance
which is given by the formula
Let us assume for a moment that 6 pictures have been taken each of them represented by a color like the ones shown in figure 17↓. The pictures have been taken evenly spaced along the stereo base from left to right in front of a subject.
To print these pictures behind a lenticular sheet they have to be interlaced. This means each picture has to be sliced in 6 parts and each slice has to be printed on a different interval. What we obtain is a big picture, usually called the master file, like the one shown in figure 18↓. Please note that the horizontal orientation of the master file changes whether we decide to print directly behind the lenticular sheet or we print in paper and then laminate.
If each sequence of 6 slices is exactly printed behind each interval of size
, these slices will be projected back by the lenticular sheet as show in figure 14↑ with no distortion. A viewer observing the lenticular print at position
,
,
,
,
,
will see exactly the pictures displayed in figure 17↑ because the light field generated by the lenticular sheet is equal to the one captured by the cameras.
This is the most common way of interlacing a sequence of pictures but it is not necessarily the only one and the correct one to be used in all cases.
Things get a bit more complicated when pictures are taken at a distance
not equal to the viewing distance
.
A lenticular sheet that is viewed at a distance
, and with a corresponding optical pitch
generates a very specific light field as shown in figure 14↑. If we want to create a realistic picture, where the virtual object printed on the lenticular sheet is as close as possible to the real object, the light field captured by the cameras must be as close as possible to the light field generated by the lenticular sheet. As shown in figure 19↓ if the target distance is larger the cameras must be placed at a greater distance because the light field produced by the object is now traveling for a larger distance. The same is true if the target distance is smaller because the light field produced by each printed distinct image has not fully converged.
Not only is the stereo base larger but the standard interlacing algorithm cannot longer be used. A more complex ray-tracing technique has to be adopted to match each ray generated by every single lenticular lens with the corresponding ray captured by any of the available cameras.
We indicate with
the size of the target and with
the difference between the required stereo base and the one predicted by equation 1↓. Referring to figure 20↑, which is a simplified version of figure 19↑, we can easily verify that
and
Both cases can be taken into account in the following stereo base equation
Scale factor
In the context of 3D Lentigraphy a light field is essentially a complex three-dimensional geometric structure composed by rays and, as such, it can be scaled up and down uniformly in all dimensions. In figure 21↓ we can see a light field produced by an unknown lenticular sheet, where we can recognize the viewing distance
and the corresponding optical pitch
, and a scaled up version.
We have already explained in the previous sections that the purpose of 3D Lentigraphy is to capture the original light field and to print it on a lenticular sheet so that the generated light field is a close approximation of the original one. In 2D photography it is very common to take pictures of an object whose real size does not match the chosen print format for example a picture of a big tree to be printed on
medium format, or a macro picture of an insect to be printed on
big format.
In 3D Lentigraphy this is the equivalent of capturing a light field which is a scaled up or down version of the one generated by the final print, which dictates the viewing distance
, the optical pitch
, and the viewing angle
. When scaling up and down the light field generated by the print, the viewing distance and the optical pitch change accordingly while the viewing angle remains constant. The stereo base and the target distance will now be calculated on the scaled light field, which is the one we want to capture.
We call
the scale factor to apply to the size of the printed object to match the size of the real one: if the size of the real object is bigger than its size on the final print we have
, if the size of the real object is smaller than its size on the final print we have
. If we refer to the print size instead of the actual object size, we can imagine a virtual scaled version of that print, which we can call the virtual target. We can then think about
as the scale factor between the final print and the scaled target.
As an example, if we take a picture of a building
tall and, on the final print, the same building is
tall, we can imagine the virtual target to be a scaled up version of the final print,
times bigger, and use it to derive all parameters required to take the picture. If the final print is a
format, the virtual target becomes approximately
.
Example – S > 1
We want to take a picture of a model waist up using an array of 5 cameras. We plan to print the interlaced image on
format paper laminated on a
lenticular sheet with a
angle of view.
We prepare a
target which is temporarily positioned in place of the real model and removed during the photoshoot. This target represents a scaled up version of the final print with a scale factor
. A real target is not strictly necessary, but we can use it to correctly position, point and focus all cameras and it is also used in post-production as a reference to remove the keystone distortion introduced by pointing the camera to the target instead of using expensive tilt-and-shift lenses.
We expect the final print to be observed approximately from a viewing distance
. Because the size of the target differs from the size of the final print we need to take into account the scale factor
and calculate a new viewing distance
.
The cameras have a focal length of
and to have the target fully visible in each frame the shooting distance must be at minimum
.
From equation 2↑ we calculate a stereo base
which is
(18%) larger than the value
predicted by equation 1↑.
Example – S < 1
Even if we plan in advance that the final print has a
angle of view and a
format, we may desire in future to print the same image on a lenticular sheet with a larger angle of view and a different format. In this scenario it is better to choose a larger stereo base: removing pictures from an existing sequence is always possible but adding new ones is not. If we do not use a larger stereo base and we later print on a lenticular sheet with a larger angle of view the final print will display a subject less deep than the original and so less realistic.
We want again to take a picture of a model waist up. We plan to print the interlaced image on
format paper laminated on a
lenticular sheet with a
angle of view. We prepare a
target that is temporarily positioned in place of the real model. This target represents a scaled down version of the final print with a scale factor
.
We expect the final print to be observed approximately from a viewing distance
. Because the size of the target differs from the size of the final print we need to take into account the scale factor
and calculate a new viewing distance
.
The cameras have a focal length of
and to have the target fully visible in each frame the shooting distance must be at minimum
, which is very different from the viewing distance.
From equation 2↑ we calculate a stereo base
which is
(83%) larger than the value
predicted by equation 1↑.
Assume that using some interpolation methods we are able to produce a sequence of 101 pictures from the 5 taken. The number of pictures to remove from the sequence, to print on the original smaller format, is given approximately by
18 pictures from both sides of the sequence.
Lenticular Depth-of-Field
In a 3D Lentigram there are objects that appear on, in front of the stereoscopic window or behind. Objects on the stereoscopic window appear fully sharp, with the maximum sharpness defined by the size of the lenses of the lenticular sheet. Objects in front of or behind the stereoscopic window appear blurred, the greater the distance from the stereoscopic window the more out of focus they appear.
This behavior is similar to the Depth-of-Field (
) in standard photography. Objects on the focal plane of the camera lens appear fully sharp, with the maximum sharpness defined by the size of the Circle-of-Confusion. Objects in front of or behind the focal plane appear out of focus. Following this idea it is possible to define the Depth-of-Field of a lenticular sheet (
) as the depth that can be stored in a lenticular sheet and perceived by the viewer as fully sharp.
The maximum sharpness of a lenticular print is limited by the size of its lenses, the mechanical pitch
. An object printed on the lenticular sheet and having a linear parallax, measured on the surface of the sheet, not bigger than
between two consecutive pictures is perceived as sharp.
The maximum number of pictures
that is possible to print behind each lens is
where
is the horizontal resolution of the printer in Pixels Per Inch and
is the optical pitch measured at a given distance
.
Considering all the pictures printed on a lenticular lens, not just two consecutive ones, the maximum linear parallax
for an object to remain sharp is given by
which becomes
where
is the resolution of the lenticular sheet in Lenses Per Inch. This means that objects that shift on the surface of the lens for a total distance bigger than
will be perceived as “jumping”. The combination of blur and jumping effects is called discretization.
Using the total linear parallax
, the lenticular angle of view
, and the viewing distance from the lenticular sheet
it is possible to calculate the quantity
, the maximum depth that can be stored in a lenticular sheet and perceived as fully sharp.
If
is the perceived depth behind the stereoscopic window (figure 24↑) the following formula applies
If
is the perceived depth in front of the stereoscopic window the following formula applies
It is easy to verify geometrically and mathematically that
, the perceived depth behind the stereoscopic window is always a bit deeper than the perceived depth in front of it.
For
both formulas can be the simplified
The total Lenticular Depth-of-Field is given by
For
the formula can be simplified to
The condition of maximum sharpness introduced with the definition of
may sound too strict for practical purposes. This condition can be weakened if the picture being printed has its own photographic
produced either with a wide aperture or by digital manipulation. If Far and Close Objects are out of focus enough to make it is impossible to calculate their total linear parallax within a single lens resolution, the value of
can be extended and so too the acceptable
Accepting 2 lenses as a condition of acceptable sharpness,
can be doubled. Accepting 3 lenses,
can be increased 3 times and so the corresponding
.
It is possible to define
,
,
as the Lenticular Depth-of-Field for a maximum acceptable linear parallax of
,
,
respectively.
The following shows a list of commercially available lenticular lenses with specifications and approximated Lenticular Depth-of-Field
| Name | (inch) | (cm) | |||
| DPLenticular | 720 | 28 | 37 | 2.74 | 6.97 |
| DPLenticular | 720 | 20 | 37 | 5.38 | 13.66 |
| Lenstar | 720 | 50 | 41 | 0.77 | 1.96 |
| Microlens | 720 | 10 | 48 | 16.17 | 41.08 |
| Microlens | 720 | 15 | 47 | 7.36 | 18.69 |
| Microlens | 720 | 20 | 47 | 4.14 | 10.51 |
| Microlens | 720 | 20 | 29 | 6.96 | 17.68 |
| Microlens | 720 | 60 | 24 | 0.94 | 2.39 |
| Microlens | 720 | 40 | 25 | 2.03 | 5.16 |
Table 1 Lenticular Depth of Field when
Example – Depth-of-Field and scale factor S > 1
In a previous example we wanted to take a picture of a model and print it on a
format paper laminated on a
lenticular sheet with a
angle of view. This requires a
target and a corresponding scale factor
. From table 1↑ we know that this specific lenticular sheet has an approximate Lenticular Depth-of-Field
.
If we printed the picture using the target size we would have a maximum linear parallax
and, because of equation ↓, a Lenticular Depth-of-Field
, the depth of the real subject that we can guarantee to appear sharp in the final print.
Example – Depth-of-Field and scale factor S < 1
In a previous example we wanted to take a picture of a model and print it on a
format paper laminated on a
lenticular sheet with a
angle of view. This requires a
target and a corresponding scale factor
. From table 1↑ we know that this specific lenticular sheet has an approximate Lenticular Depth-of-Field
.
If we printed the picture using the target size we would have a maximum linear parallax and, because of equation ↓, a Lenticular Depth-of-Field , the depth of the real subject that we can guarantee to appear sharp in the final print.
If we printed the picture using the target size we would have a maximum linear parallax and, because of equation ↓, a Lenticular Depth-of-Field , the depth of the real subject that we can guarantee to appear sharp in the final print.
It is interesting to notice that while in this example the lens has a potential Depth-of-Field that is larger than the one in the previous example, because of the magnification the area of the subject that can be displayed fully sharp on the final print is actually reduced.
Depth and Lenticular Depth-of-Field
The Lenticular Depth-of-Field is an indicator of how much depth is in focus for a specific lenticular sheet. A lens with a great Lenticular Depth-of-Field allows the creation of a deeper image, but the correlation between Depth and Lenticular Depth-of-Field is often misunderstood and the two properties often confused one for another.
Let us assume we have captured the lightfield produced by an object with a sequence of 100 pictures taken with a camera slider and we want to print an interlaced image at
. If we use the most common interlacing process, select a subset of 18 pictures (0, 6, 11, 16, …, 100) and print the interlaced image on a
lenticular sheet with a
angle of view, we know that the available Lenticular Depth-of-Field is approximately
. If we select another subset of 12 pictures (0, 8, 16, 25, …, 100) and print the interlaced image on a
lenticular sheet with a
angle of view we know that the available Lenticular Depth-of-Field is approximately
.
The first
print has a greater Lenticular Depth-of-Field and more of the image depth will appear in focus. Because both lenses have the same Angle of View and because the pictures at the extremes of both sequences are the same, 0 and 100, the measure of their parallax measured on the prints are the same and so is the perceived depth. The lightfield generated by the second
print is similar to the one produced by the first print with fewer principal rays as shown in figure 25↓.
Which of the two lenticular sheets to prefer depends on the image to print. If the image is not very deep a
lenticular sheet may be preferable. If the original image is deeper but contains an existing Photographic Depth-of-Field, either introduced by the camera objective or artificially created with artistic intentions, the
lenticular sheet may still be the right choice. The same applies for an image which contains blurred elements by nature like fire, clouds or smoke.
Some viewers may also opt for an image printed on a
instead of a
, preferring a higher resolution print instead of a greater Lenticular Depth-of-Field.

























In my experience 60 and 40 lpi lenses are very low resolution. Those are typically meant for viewing from afar, like a bus shelter. For hand held pieces, like a DVD cover you would definitely use a 100 lpi lens.
ReplyDeleteMany photographers, with low volume production, use inkjet printers which have usually a resolution around 720PPI when printed on on paper. This limits the LPI that can be used. I use 60LPI for postcard and 40 for 13"x19" prints.
DeleteIn figure 8 you show the cameras at different angles. I would never do that. Instead I move the camera in precise increments (depending on how much parallax I want) along a FOBA stand. Then in Photoshop I can key the images in to exactly where I'd like the zero point in space to be.
ReplyDeleteI use a toe-in approach and then remove the keystone distortion in post production. It gives me more creative control during a photo shoot. Keeping the cameras parallel work too but you will have to crop the images later and loose resolution. Both are valid approaches. In macro photography I use a 3rd approach, a camera rotating around the subject.
DeleteHave a look at the final result here: www.framedlives.com
All Hollywood 3D movies are shot toed-in and the vertical parallax is removed in post. Clearly this is a valid way of working, saving resolution at the expense of post production. More than 1 way.
ReplyDelete